Project Grant 2020
Type theory for mathematics and computer science
Principal investigator:
Thierry Coquand, Professor of Computer Science
Co-investigator:
Stockholm University
Peter LeFanu Lumsdaine
Institution:
University of Gothenburg
Grant in SEK:
SEK 34.7 million over five years
Imagine a map of the world. The “four-color theorem” states that no more than four colors are needed to color the map so that no regions sharing a common boundary share the same color.
The theorem was presented in the 19th century, but proving it has not been easy. Several attempts were published and then found to be incorrect before a team of mathematicians succeeded in the 1970s.
The problem was that the proof took up several hundred pages, and was based on analysis of millions of cases that could not be performed by hand. Scrutinizing and verifying the proof was essentially impossible.
Errors creeping in
The four-color theorem illustrates the problem that it may be impossible for mathematicians to examine each other’s proof – with the risk of errors creeping in as a worrying consequence. The problem also applies to computer software.
“It’s very difficult to check whether software is computing correctly just by looking at it,” says Coquand, who is a professor of data and information technology at the University of Gothenburg.
One way out is therefore to enlist the help of computers when scrutinizing proof. Coquand is leading a project funded by Knut and Alice Wallenberg Foundation with the purpose of developing “interactive proof systems” – software that helps to verify the correctness of mathematical reasoning.
“Proof systems can systematically go through proof and check that all steps are correct. But our goal is that they should also be able to help create proof and suggest steps that can be included to the user.”
As mentioned, the four-color theorem is an example of a mathematical theorem whose proof has been verified using an interactive proof system. Systems of this kind have also been used to check software known as a “compiler”. The correctness of such software is crucial in some applications, e.g. in avionics.
Mathematical language the computer understands
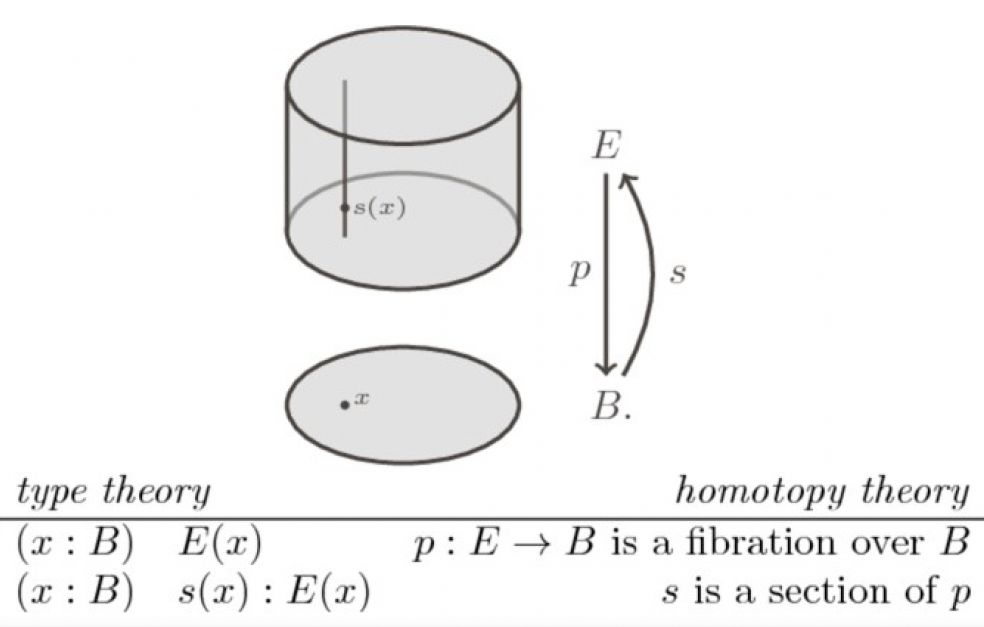
The basis for these proof systems lies in a field called “type theory”, in which the Swedish logician Per Martin-Löf is one of the leading figures. A mathematician writing proof often uses elements of informal language and intuition. But this does not work when a computer has to check the proof. In the 1970s Martin-Löf created a formal language that can be used to express mathematics and that serves as a link between mathematical proof and computer programs.
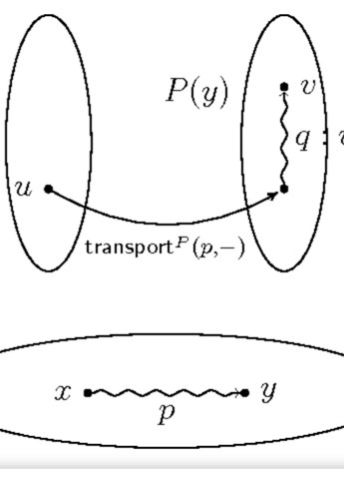
In recent years this reasoning has been elaborated by the Russian–American mathematician Vladimir Voevodsky, who made new ground-breaking discoveries in type theory. Voevodsky discovered a connection between type theory and one of his own specialist fields in mathematics, known as homotopy theory.
“It was a completely new and entirely unexpected connection, which has implications for the very fundaments of mathematics. It paved the way for new opportunities to improve existing proof systems and their use.”
Voevodsky’s univalent foundation of mathematics describes methods of identifying one mathematical object using another. Such identifications are important in order to be able to automatically reuse mathematical theorems and parts in computer software.
Vital for secure encryption
The present research project is rooted in Voevodsky’s theories, and is examining them further. The aim is to improve interactive proof systems so they can be used to process abstract mathematics as well, which is essential for many mathematical problems and applications.
“Encryption, for instance, uses highly abstract mathematical concepts. If we want to be sure that the algorithms used for encryption purposes are correct, we must also be able to express such concepts in proof systems. Modern proof systems are impressive, but, until Voevodsky’s contributions it was not clear how to represent in such systems some contemporary abstract mathematical notions.”
Coquand laid the foundations for this project in his earlier research as a Wallenberg Scholar.
“We have been able to explain Voevodsky’s axiom of univalence in a computational way. The goal of the present project will be to explore further these connections and to design proof systems where abstract contemporary mathematical notions and computations are expressed in a uniform way.”
The research is a joint project between Coquand and Peter LeFanu Lumsdaine, a mathematician at Stockholm University. They are also collaborating with researchers in a major U.S. project addressing the same issues.
By the end of the five-year project, the Swedish researchers hope to have improved current proof systems to the point where they can deal with mathematical concepts of interest to working mathematicians.
Text Sara Nilsson
Translation Maxwell Arding
Photo Institut des Hautes Etudes Scientifiques