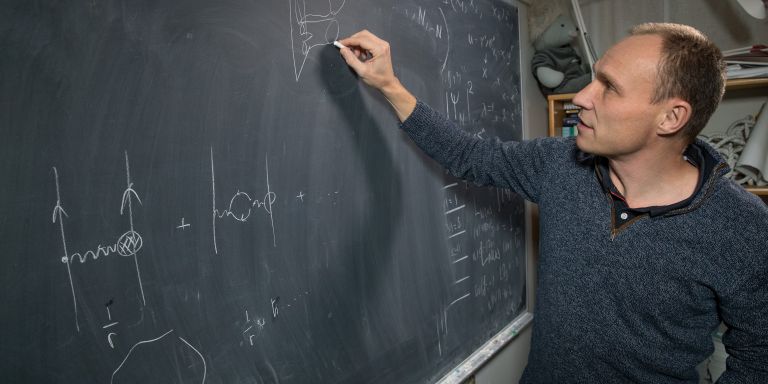Wallenberg Scholar Tobias Ekholm devotes his time to problem-solving at the border between mathematics and physics where there may be answers that provide new insights into major mysteries of the universe. Among other things, he is using symplectic geometry to explore string theory.
Tobias Ekholm
Professor of Mathematics
Wallenberg Scholar
Institution:
Uppsala University
Research field:
Topology, differential geometry, and symplectic geometry with relevance to theoretical physics, particularly in the fields of string theory and quantum field theory.
Ekholm has always been interested in both mathematics and physics – subjects with a long common history.
“In the eighteenth century virtually no distinction was drawn between mathematicians and physicists. Now the subjects are merging once again. We address many of the same problems, and different approaches are fruitful for both sides.”
Tobias explains that research collaboration enables scientists to benefit from each other’s strengths:
“Mathematicians follow a stringent tradition with proofs down to the last detail, whereas physicists are more liberal, and use a bigger toolbox to identify the important structures.”
A wilder form of geometry
One interdisciplinary field is symplectic geometry, a flourishing branch of mathematics that Tobias came across while working as a postdoc at Stanford around the turn of the millennium. Symplectic geometry is some distance away from traditional schoolbook geometry. It is a “wilder” form of geometry in which certain two-dimensional areas must remain unchanged during manipulation.
The term was coined in the 1800s, when William Hamilton, an Irish mathematician, reformulated classical Newtonian mechanics, which for example explains planetary orbits or how an apple falls. Before Hamilton’s work, complicated calculations was needed to describe these motions, but Hamilton gave the formulas a geometrical language, making the equations easier to solve. A symplectic surface became a measure of the two interlaced manifolds: position and velocity, a two-dimensional geometry.
“The Wallenberg Scholar grant is helping to build a strong mathematical environment at an advanced level. Among other things, we can now attract pre-eminent postdocs from universities such as Stanford, Princeton and Berkeley. Uppsala is suddenly on the world map, and we are becoming part of the global research infrastructure.”
Knotted problems
But symplectic geometry can also be used to study more dimensions – four, six, and so on, which has rekindled interest in the field. Modern symplectic geometry has links to a field of mathematics called topology, and particularly the study of knots.
“Mathematical knots are formed by interlacing and looping a piece of string and then joining its ends.”
The number of knots is infinite, and one of the challenges is to find new calculable methods of differentiating them. A surprising coincidence occurred a few years ago. Tobias and his colleagues managed to identify a formula from a mathematical viewpoint, while physicists had discovered the same formula from their perspective.
“At first we couldn’t understand how we could arrive at the same conclusion. It was new to them and to us, but a novel and striking relationship between symplectic geometry and topological string theory had been established.”
Almost like science fiction
The breakthrough has provided the impetus for further research on the border between mathematics and string theory. The work includes combining theories capable of shedding light on difficult problems. One example is an observation from the world of physics, known as “gauge-string duality”.
“It’s a fantastic prediction that links gauge theory with string theory, and to a mathematician sounds like something out of science fiction.”
The problem was presented for the first time in the late 1990s, and has since been a central topic in the world of mathematics and physics.
“But no one has really grasped how it works, and I never thought we would fully understand it. But in 2018 we did actually manage to explain it mathematically, and we have also identified a mechanism that may be of benefit in several areas.”
The results also pave the way for a new understanding of “M-theory”, which is a way of unifying the various versions of string theory.
“We can see signs that M-theory exists, although it is obscured. But this new understanding will enable us to gain an idea about the nature of topological M-theory, and that will open up exciting perspectives.”
Attractive research environment
Over a period of ten years the Wallenberg Scholar grant has provided financial stability, enabling the establishment of an internationally attractive research environment.
“Now we can offer some of the most talented people positions as postdocs and visiting researchers. We also have the funds to arrange conferences that attract some of the biggest names.”
One example is the annual String Math conference, which in summer 2019 was held in Uppsala. Speakers included three recipients of the Fields Medal, one of the most prestigious awards in the mathematics, and three Breakthrough Prize winners.
Personal meetings and exchange of knowledge are important. Tobias sees a role model in Yakov Eliashberg, a seminal figure in the field of symplectic geometry.
“He has meant a lot to me, and has an approach to the subject that is hard to describe in words, but could be compared to the way a writer or a composer approaches their work.”
Sometimes deep-rooted traditions can even be seen in body language. Tobias watched one of his supervisors pacing in front of the blackboard:
“I’ve seen exactly the same characteristic way of walking in other prominent researchers with the same background, and I can only imagine how far back in time these shared traits can be traced. There is a culture in mathematics that is passed down through the generations,” he concludes.
Text Nils Johan Tjärnlund
Translation Maxwell Arding
Photo Magnus Bergström