
Wushi Goldring
Associate Professor of Mathematics
Wallenberg Academy Fellow 2019
Institution:
Stockholm University
Research field:
Algebraic group theory as a universal language
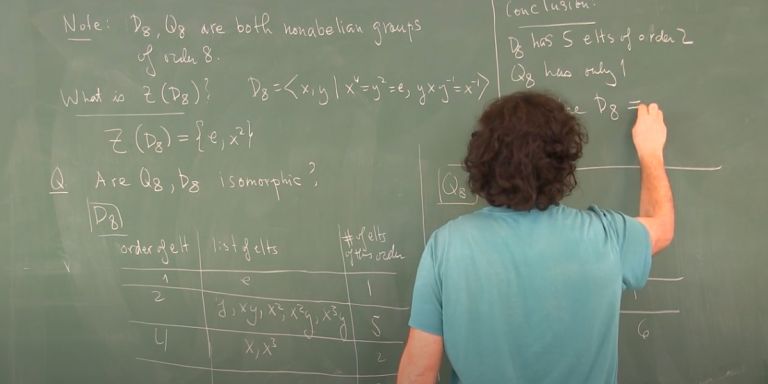

Wallenberg Academy Fellow 2019
Institution:
Stockholm University
Research field:
Algebraic group theory as a universal language
The first discoveries in group theory were made over two hundred years ago. The theories have applications in many branches of mathematics, and have also contributed to strides made in quantum physics, chemistry and molecular biology.
“Groups are already recognized in mathematics as being extremely powerful and of great use in various fields. I want to show that their role is even more basic and more fundamental than was previously thought,” Goldring says.
He draws a parallel with one of his interests – travel – to explain what he is looking for.
“When you travel, you want to have few things which are light and fit into a small backpack – things you can use wherever you are. As a mathematician, I try to imagine the objects known as groups in the same way: a toolkit which is small and light and works in numerous situations.”
Mathematics students usually come across the theory of algebraic structures known as groups for the first time as they approach the end of their Bachelor studies. This is also true at Stockholm University, where Goldring has taught and led a research team since 2016.
“I would like to see group theory taught earlier. This is because I think that subjects currently learned early – such as derivatives, integrals and measurement of areas – are easy for some people. But for other people, like me, it is easier to think in terms of groups.”
“I am proud that we have such a diverse mathematics department at Stockholm University with researchers from all over the world, and by hiring PhD students and postdoctoral researchers, the grant allows me to contribute toward the growth and prosperity of this research environment."
Focusing on universal phenomena comes easy to Goldring, not only in his research, but also when discussing politics or movies, for example.
“I try to zoom out and see if what is happening specifically is part of a larger context. Group theory is an excellent opportunity for that kind of thinking in mathematics. Any object studied – whether it arises from numbers, geometry or analysis – has groups associated to it. Objects from completely different mathematical fields can have the same groups associated to them, and I want to see if they share other traits as well.”
Goldring explains that group theory is often called the language of symmetry. When a mathematical object appears to be symmetrical, group theory can be used to analyze it. He holds up a folded square piece of paper to demonstrate the connection between symmetry and groups.
“It can be rotated but it can also be flipped, or both. All conceivable ways in which the paper can be moved while keeping the same shape can be seen as a group.”
Normally speaking, i.e. when we are not in the midst of a pandemic, Goldring enjoys sitting in cafés working.
“It’s easy to get stuck if you just sit and think in front of a computer in your office. Taking a walk to a café provides the brain with much needed fresh air.”
Visiting cafés was also a family tradition when Goldring was growing up in Los Angeles and on trips to Europe. His mother has a PhD in mathematics, and his father is a professor of philosophy relating to physics and mathematics, so the conversations often turned to mathematics and its role in the world.
But his parents did not push him to become a mathematician. “That would probably have had the opposite effect”, he says laughing. However, they did notice that he was bored and unhappy at school, especially in math classes, so they arranged for him to enroll on courses at UCLA when he was still in middle school. It was a turning point. He completed his first research project as a teenager, and later received his PhD from Harvard.
The person who inspired him to become a researcher in mathematics was Serge Lang, a well-known mathematician successful in number theory.
“We met when he was in his late seventies, and I was sixteen. Sadly, he died just a year later, but our mathematical interaction – an apprenticeship of sorts – was a life-changing experience for me.”
Recently Goldring has become increasingly interested in “reductive groups”, which are groups of matrices.
“I spend a lot of time multiplying, inverting and calculating matrices – really elementary things that you learn to do at university. It’s interesting that these reductive groups consist of matrices that many have heard of, but that they also have deeper properties. I like areas of mathematics where you can study the same objects at different levels.”
Having worked at a number of top universities in the U.S. and Europe, Goldring has now settled down in Stockholm. He appreciates the multifaceted and vibrant research environment in the department of mathematics. The grant he has received from Knut and Alice Wallenberg Foundation enables him to recruit more postdocs and PhD students, who can help in developing a general theory on how mathematical objects can be constructed by groups.
“It also gives me an opportunity to meditate on what I really want to do. I can take more risks and focus more on long-term projects which may take several years.”
Text Susanne Rosén
Translation Maxwell Arding
Photo Department of Mathematics, Stockholm University, Markus Marcetic