Modin’s PhD thesis in computational mathematics focused on developing new methods of using the computer to solve scientific problems.

“Most problems occurring as differential equations in science cannot be solved exactly. There are very few problems to which we can find analytical solutions,” Modin says.

Scientists instead enlist the help of the computer and well-established approximation methods. In his thesis, Modin elaborated methods that preserve the underlying geometric properties of Hamiltonian dynamics – a major class of problems in physics.

During his time as a postdoc at Massey University in New Zealand he discovered how the framework underlying Hamiltonian systems also has a bearing on shape analysis, which is a fairly new branch of mathematics.

“In shape analysis we use the same type of mathematics – Hamiltonian systems – that I used in my doctoral thesis. The common framework enables us to understand the flows associated with shapes. So it was obviously a field worth exploring.”

Medical applications

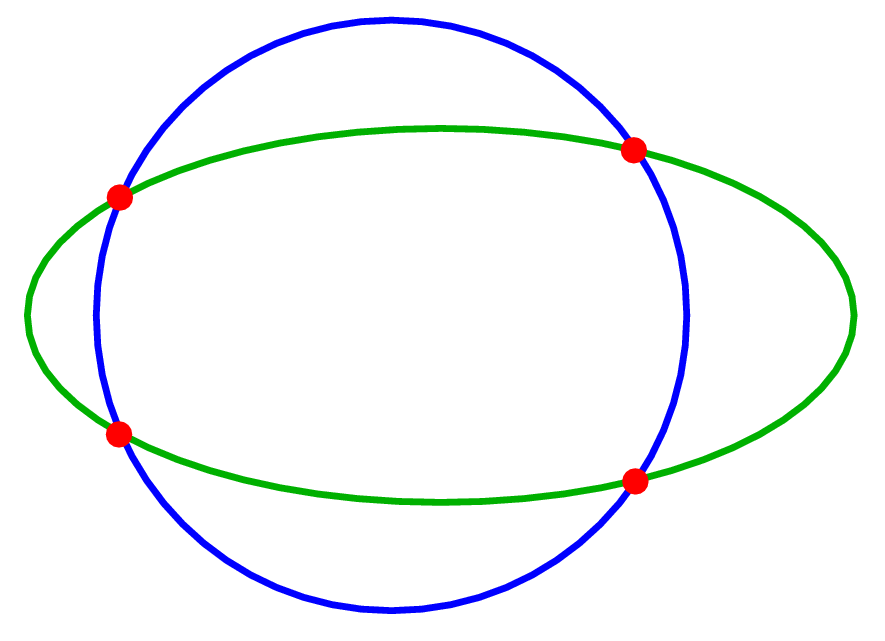
One of the founders of shape analysis was the Swedish professor Ulf Grenander. He quickly realized its potential medical applications, particularly in comparing images of our internal organs. New mathematical tools are needed to interpret three-dimensional MRI images. Here, shape analysis offers an advantage by offering a pure mathematical comparison of different shapes. One of the simplest examples is to ascertain what distinguishes a circle from an ellipse.

“Shape analysis provides us with a tool to deform one shape – a circle, for example – to the other shape – an ellipse, for example – and then measure the ‘size’ of the deformation. This yields a mathematical distance between the two shapes,” Modin explains.

The field makes use of Riemannian geometry – the mathematical field about the shortest distance between points on curved surfaces – and is also closely related to classical fluid mechanics.

Stepping over to AI

Modin has already made a number of strides since he received the Wallenberg Academy Fellow grant. They include progress in understanding the relationship with fluid mechanics. He has also started to use shape analysis tools in the field of deep learning, which is a branch of machine learning. Deep learning makes use of artificial neural networks to mimic the way the human brain processes information. Increasing use of AI is being accompanied by broader applications for deep learning, despite the fact that it has not yet been ascertained exactly how the method actually works.

“The Wallenberg Academy Fellow grant gives me the opportunity to adopt a long-term approach to solving knotty mathematical problems with real-world applications.”

Modin can now see potential for learning more and also designing better algorithms by enlisting the help of mathematical tools used in shape analysis.

Gentler radiotherapy

He is keen to bring the theoretical progress he has made to projects with more tangible applications – particularly in the medical field. One example is a project being conducted in collaboration with a research team at the University of Utah in the U.S. for gentler radiotherapy.

When a lung tumor is irradiated, the aim is to avoid damaging surrounding tissue. But even if the patient remains motionless during the treatment, the tumor moves around continually as breathing inflates and deflates the lung.

“At present, tumor movements are ignored. An average point is calculated. This is then irradiated, destroying part of the surrounding tissue. Here, shape analysis has shown itself to be a useful mathematical strategy for developing algorithms capable of contributing to more accurate radiotherapy,” Modin explains.

He hopes to start similar projects in which basic research can pave the way for more applications, preferably here in Sweden, in collaboration with Sahlgrenska University Hospital.

“Close collaboration is especially important in developing medical applications. Visiting the clinical environment makes it easier to understand the problems.”

Arousing curiosity

Modin chose mathematics fairly late in life, and says he has always been bad at counting. But he gained a vital insight during a university course in linear algebra:

“Mathematics at university level is quite different from what you learn in grade school and high school. At university it’s all about understanding different structures, and using theories and frameworks to solve problems. It was a real epiphany for me,” he says.

He is keen to pass on the experience, and enjoys presenting his research to a wider public.

“I hope to motivate young people to choose science by arousing their curiosity. Curiosity is the foundation of all research,” he concludes.

Text Magnus Trogen Pahlén
Translation Maxwell Arding
Photo Mikael Terfors