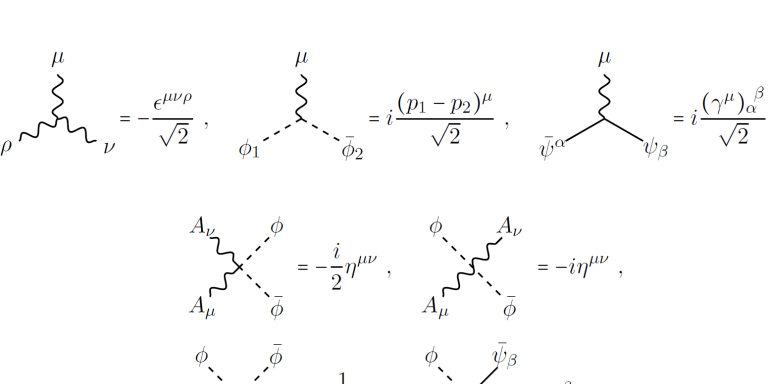Over a hundred years ago Einstein formulated his theory of general relativity. Quantum mechanics is of the same age. No physicist has yet reconciled the two into a theory of quantum gravity that can be confirmed experimentally. Wallenberg Academy Fellow Henrik Johansson is working on new mathematical tools that may address the challenging problem, and give us a better understanding of the universe at a fundamental level.
Henrik Johansson
PhD, Particle Physics
Wallenberg Academy Fellow, prolongation grant 2018
Institution:
Uppsala University
Research field:
New mathematical descriptions unifying quantum mechanics and general relativity
It happens that Johansson sits down with a pen and paper and makes his calculations entirely by hand. More advanced equipment is not needed for the research. His field is a highly theoretical corner of science.
“We are a few hundred researchers in the world with my specialization. And, I know, at a personal level, the authors behind many of the articles that I read.”
Over the past few years Johansson has established a large and lively research team working on quantum field theory, supergravity and string theory at the Ångström Laboratory in Uppsala. The initiative has been made possible by funding from Knut and Alice Wallenberg Foundation. The team now comprises some ten or so people, representing about a quarter of the division of theoretical physics. Visitors are usually impressed by the research environment.
“A larger team means we get more done in the project, but the most important aspect is of course the quality of researchers, rather than the quantity. We have managed to attract some very talented people.”
Reconciling the irreconcilable
Johansson and his colleagues are addressing a problem that physicists have been trying to solve for years: to unify Einstein’s theory of general relativity with quantum mechanics. Both theories are needed for the understanding of a wide range of phenomena: from elementary particles to the birth of the universe.
But the mathematics falls short. One stumbling block is that infinite numbers appear in calculations when the theories are combined. The dream is to formulate a new mathematical description capable of giving finite answers and reliable results.
Improved theoretical understanding is becoming ever more important as major strides are made with experiments. The Higgs particle was detected in 2012 with the help of the Large Hadron Collider (LHC) at CERN. Three years later researchers at the Laser Interferometer Gravitational Wave Observatory (LIGO) were able to confirm Einstein’s predictions by detecting gravitational waves produced by two colliding black holes.
The findings open a new window to the universe, but more effective mathematical tools are needed to exploit the full potential.
“Experimental research is becoming ever more dependent on advanced and precise calculations.”
In recent years Johansson has been working hard to develop new methods that radically simplify the calculations. He has found that the same mathematical objects can be used to describe physics at widely disparate scales: from the most miniscule processes in the universe – such as collisions between elementary particles – to massive occurrences – such as colliding black holes.
“The underlying mathematical description is almost identical.”
Making impossible calculations possible
The current project is based on a breakthrough made by Johansson and two U.S. colleagues more than ten years ago. They were studying gravity together with gauge theories, which describe the three other fundamental forces in the universe, and found a previously unknown connection.
The same mathematical objects, known as Feynman diagrams, can both describe gravitons – carriers of gravitational force – and gluons – carriers of the strong force in particle physics. The discovery paved the way for a new field of research.
“It’s an enormous help that we can use the same mathematical description. The advantage is that we can reduce the number of computation steps, which in turn means we can perform calculations that were previously considered impossible.”
Following the observation of gravitational waves, new mathematical tools are needed to describe black holes with extreme precision: how they interact, approach, radiate gravitational waves, and eventually collide.
“We want to be able to describe exactly how the gravitational wave frequency changes as two black holes approach one another.”
The researchers are using quantum mechanical perturbation theory. So far they have reached the second or third order, but that is only halfway there.
“We anticipate that we’ll need to reach the sixth order eventually – much theoretical work remains to be done.”
“Over the past few years we have built up a strong research team made up of postdocs and PhD students of a high caliber. We have an unusually large team, internationally speaking, and without the support of Knut and Alice Wallenberg Foundation, it would not have been possible to create this research environment.”
Measurements in curved space
Another part of the project is attempting to describe gravitational waves in the early universe. This was a time when the universe likely expanded exponentially, according to the inflation hypothesis, which means by Einstein’s equations that the universe can be described as a curved space, known as the de Sitter space.
The researchers are making use of scattering amplitudes, otherwise used for particle collisions, to determine the correlation between different points in the de Sitter space, and to calculate fluctuations in the cosmic microwave background.
“We think we can use the same tools, by making use of gauge theories in curved space, to try to describe gravitational waves in the early universe.”
Many researchers hope it will eventually be possible to replace Einstein’s theory with an entirely new theoretical framework.
“I’m not convinced that it will happen anytime soon, but even within Einstein’s theory many practical improvements are currently needed. This is where my research can make a contribution,” says Johansson.
Text Nils Johan Tjärnlund
Translation Maxwell Arding
Photo Henrik Johansson, Ingrid Holm