Fredrik Viklund är professor i matematik vid KTH och Wallenberg Scholar. När han berättar om sin forskning nämner han ofta ett ord: samspelet. Det är nämligen i mötet mellan matematik och fysik som många av de intressantaste upptäckterna sker.

– Vi kan formulera fysikens lagar med hjälp av matematik på ett förvånansvärt effektivt sätt, säger Fredrik Viklund.

Och för det krävs ingen avancerad utrustning – en stor del av forskningen bedrivs med papper och penna.

Viklund arbetar bland annat med ett område som kallas stokastisk konform geometri – en gren av matematiken som växte fram i början av 2000-talet. Den beskriver slumpmässiga geometriska strukturer, som först upptäcktes i fysikens modeller av till exempel porösa material eller magnetism.

Det visar sig att till synes helt olika fenomen i naturen delar samma typ av slumpartad, men ändå förutsägbar, geometri.

– De här objekten är mycket oregelbundna. Men de har också symmetrier som vi kan utnyttja. Det öppnar för nya sätt att förstå både matematik och fysik, säger Viklund.

Linjerna i sådana objekt är inte raka som i en linjal, utan utgörs av skakiga kurvor som påminner om ett kustlandskap i närbild. Men här finns också dolda symmetrier som forskarna kan utnyttja. När man förstorar, vrider och sträcker på objekten kan de bete sig på ett ordnat sätt. Att hitta och använda de symmetrierna är en nyckel i forskningen.

Broar mellan områden

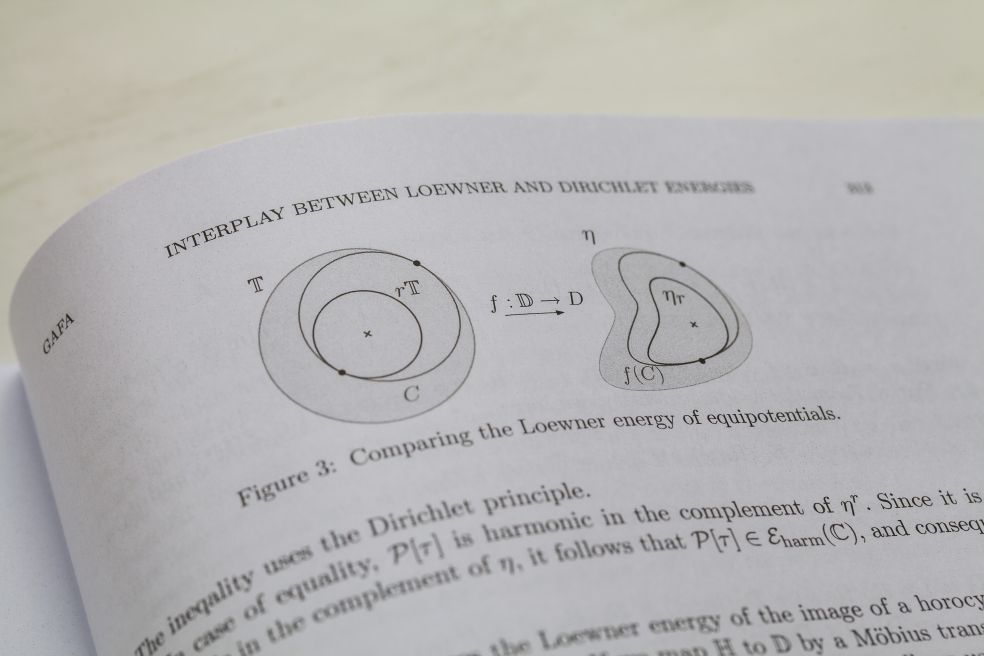
En central del i Viklunds forskning går också ut på att bygga broar mellan olika matematiska områden. Ett exempel är den så kallade Loewnerenergin. Den kan beskrivas som ett mått på hur mycket en sluten kurva avviker från att vara en perfekt cirkel. Ju mer kurvan dras ut, snörps åt eller fransar sig, desto högre blir energin.

Loewnerenergin kan tolkas både med hjälp av sannolikhetsteori och via mer klassisk analys, och binder därmed samman två världar som tidigare betraktats som helt åtskilda.

– Det är spännande när man hittar oväntade samband mellan områden som egentligen inte har något med varandra att göra. Då uppstår nya verktyg och nya frågor att utforska, säger Fredrik Viklund.

Matematiken fascinerar mig. Den är väldigt kraftfull och ger oss verktyg för att tänka och prata om annars ofattbara begrepp, till exempel oändligheten.

En annan del av Viklunds arbete rör kvantfältteorier. Det handlar om matematiska modeller som används för att beskriva elementarpartiklar och deras växelverkan, till exempel i standardmodellen. Ett viktigt exempel är Yang-Mills-teorier.

Här finns en mängd spännande och svåra problem som inte är så väl utforskade av matematiker ännu. Men på sikt kan det bli möjligt att ta fram bättre ”kartor” över naturens minsta byggstenar.

– Det är ett växande område och det är troligt att nya metoder kan föra forskningen framåt, säger Fredrik Viklund.

Stöd för risktagande forskning

För Fredrik Viklund har stödet från Knut och Alice Wallenbergs Stiftelse varit avgörande. Som Wallenberg Academy Fellow och senare Wallenberg Scholar har han fått både tid och resurser att bedriva långsiktig forskning.

– Jag har kunnat fokusera på svårare problem och vågat ta större risker. Och jag har också fått möjlighet att anställa doktorander och postdoktorer för att bygga upp en stark forskningsmiljö. Samtidigt har stödet gjort det möjligt att samarbeta mer med andra unga forskare utanför mitt eget ämne, berättar han.

Viklund framhåller att just nätverket och de återkommande mötena mellan forskare inom olika fält har varit ovärderliga.

– I Sverige finns egentligen ingen naturlig mötesplats för framstående forskare över ämnesgränserna. Det här programmet har skapat just det, och det har betytt väldigt mycket för mig, säger han.

Svårt att förutse genombrotten

För många är matematikforskning ganska abstrakt och det är inte alltid forskaren kan ge svar på hur forskningen ska användas.

– Jag bedriver grundforskning. De stora framstegen går inte att förutse – kunde man det vore de redan gjorda. Men utan grundforskning hade vi aldrig haft de verktyg som tillämpad forskning bygger på. Det är därför ett långsiktigt stöd är så viktigt.

Vetenskapshistorien visar att när matematiker hittar nya samband mellan skilda områden leder det ofta fram till oväntade verktyg som senare blir viktiga även utanför matematiken.

Här finns dessutom en nära koppling till fysiken. Bättre matematiska modeller kan ge en djupare förståelse av kvantvärlden, vilket på sikt påverkar allt från materialvetenskap till teknik.

För Fredrik Viklund handlar mycket av tillfredsställelsen även om den upptäckarglädje som forskningen ger och om att få se nya samarbeten växa fram.

– De senaste åren har vi fått uppleva en blomstring inom svensk matematik. Nu har vi en miljö som är väl så stark som någon annanstans i världen och det är oerhört stimulerande att få vara en del av den utvecklingen.

Text Nils Johan Tjärnlund
Bild Magnus Bergström