Projektanslag 2020
Type Theory for Mathematics and Computer Science
Huvudsökande:
Thierry Coquand, professor i datalogi
Medsökande:
Stockholms universitet
Peter LeFanu Lumsdaine
Lärosäte:
Göteborgs universitet
Beviljat anslag:
34,7 miljoner kronor under fem år
Tänk dig en karta, till exempel över världens länder. Det behövs högst fyra färger för att färglägga kartan så att inga angränsande regioner får samma färg. Detta säger ett matematiskt teorem som kallas fyrfärgssatsen.
Teoremet presenterades på 1800-talet, men att bevisa det har inte varit lätt. Flera felaktiga bevis publicerades innan en grupp matematiker på 1970-talet lyckades ta fram ett korrekt bevis.
Problemet var att beviset blev hundratals sidor långt och byggde på analys av miljontals fall, som inte gick att genomföra för hand. Att granska och kontrollera beviset var i princip omöjligt.
Fel kan smyga sig in
Fyrfärgsteoremet illustrerar problemet att det kan vara omöjligt för matematiker att granska varandras bevis – med risken att fel smyger sig in som oroväckande följd. Problemet gäller också datorprogram.
– Det är mycket svårt att kontrollera om datorprogram räknar rätt enbart genom att titta på programmet, säger Thierry Coquand, som är professor i data- och informationsteknik vid Göteborgs universitet.
En utväg är därför att ta datorer till hjälp för granskningen. Thierry Coquand leder ett projekt som, med finansiering från Knut- och Alice Wallenbergs Stiftelse, arbetar med att utveckla så kallade interaktiva bevissystem – datorprogram som hjälper till att kontrollera riktigheten i ett matematiskt resonemang.
– Bevissystem kan systematiskt gå igenom ett bevis och kontrollera att alla steg är korrekta. Men vårt mål är att de också ska kunna hjälpa till att bygga bevis och föreslå användaren steg som kan ingå.
Fyrfärgsteoremet, som nämndes tidigare, är ett exempel på en matematisk sats vars bevis har kontrollerats med ett interaktivt bevissystem. Sådana system har också använts för att kontrollera programvara. Till exempel en så kallad kompilator, vars riktighet är avgörande inom bland annat flygelektronik.
Använder språk för matematik som datorn förstår
Grunden för dessa bevissystem finns inom ett område som kallas typteori, där den svenske logikern Per Martin-Löf är en förgrundsperson. När en matematiker skriver ett bevis använder han eller hon ofta inslag av informellt språk och intuition. Men det fungerar inte när en dator ska kontrollera beviset. På 1970-talet skapade Per Martin-Löf ett formellt språk som kan användas för att uttrycka matematik, och fungerar som en koppling mellan matematiska bevis och datorprogram.
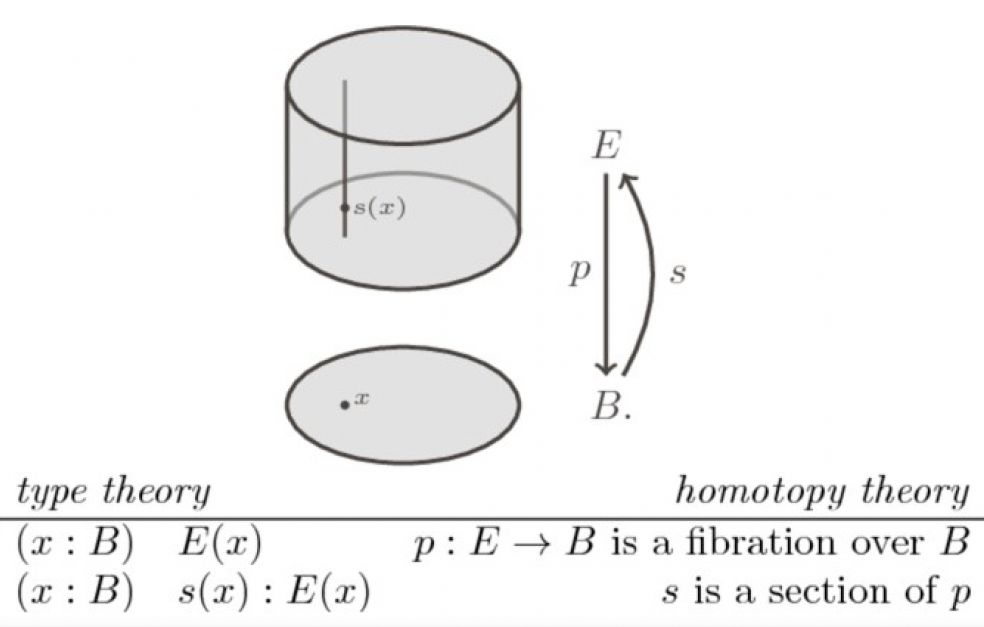
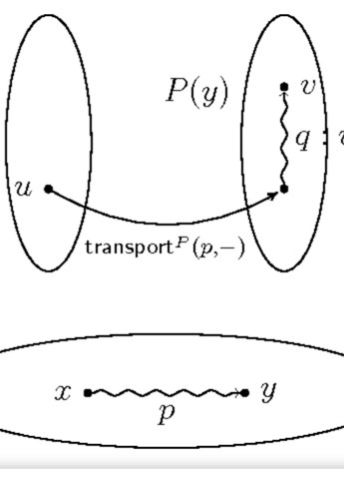
Dessa resonemang har på senare år utvecklats av den rysk-amerikanske matematikern Vladimir Voevodsky, som kom på nya banbrytande upptäckter kring typteori. Voevodsky upptäckte ett samband mellan typteori och ett av hans egna specialområden inom matematiken, så kallad homotopiteori.
– Det var en ny och helt oväntad koppling som har konsekvenser för matematikens själva grundvalar. Den öppnade för nya möjligheter att förbättra de existerande bevissystemen och deras användning.
Voevodskys så kallade univalenta grundval för matematiken, handlar om metoder för att identifiera ett matematiskt objekt med ett annat. Sådana identifikationer är viktiga för att automatiskt kunna återanvända matematiska teorem och delar i datorprogram, förklarar Thierry Coquand.
Viktigt för säker kryptering
Det aktuella forskningsprojektet tar avstamp i Voevodskys teorier och undersöker dem vidare. Målet är att förbättra de interaktiva bevissystemen så att de ska kunna användas för att hantera även abstrakt matematik, vilket är viktigt för många matematiska problem och tillämpningar.
– Inom exempelvis kryptering används väldigt abstrakta matematiska begrepp. Om vi vill vara säkra på att de algoritmer som används inom kryptering är rätt, måste vi kunna uttrycka även sådana begrepp i bevissystemen. Dagens bevissystem är imponerande, men innan Voevodsky var det inte klart hur vissa nutida abstrakta matematiska begrepp skulle hanteras i sådana system.
I sin tidigare forskning som Wallenberg Scholar, har Thierry Coquand lagt grunden för arbetet.
– Vi har lyckats förklara Voevodskys univalensaxiom på ett beräkningsmässigt sätt. Målet för det här projektet är att undersöka de kopplingarna vidare och designa bevissystem där abstrakta matematiska begrepp och beräkningar uttrycks på ett enhetligt sätt.
Forskningsprojektet är ett samarbete mellan Thierry Coquand och matematikern Peter LeFanu Lumsdaine vid Stockholms universitet. De samarbetar också med forskare i ett stort amerikanskt projekt som arbetar med samma frågor.
När projektets fem år är till ända hoppas de svenska forskarna ha förbättrat dagens bevissystem så att de kan hantera matematiska begrepp som är intressanta för arbetande matematiker.
Sara Nilsson
Bild Institut des Hautes Etudes Scientifiques